How To Find Z Score In R
Alright, let's talk Z-scores in R. If you're used to tinkering with your engine's performance or analyzing dyno data, understanding how to standardize data using Z-scores is a crucial skill. It's like calibrating your gauges – you need a standard reference point to compare against. We're going to dive into the nitty-gritty of calculating Z-scores, why it matters, and how to do it efficiently using R.
Purpose: Why Z-Scores Matter
Think of Z-scores as a universal translator for your data. Just like you might use a common unit like horsepower to compare different engine configurations, Z-scores allow you to compare data points from different distributions.
Why is this useful? Imagine you're comparing the fuel efficiency of two different cars. One's measured in MPG (miles per gallon) and the other in L/100km (liters per 100 kilometers). You can't directly compare them, right? You need to convert them to a common scale. That's what Z-scores do. In statistical terms, it's about standardizing your data to a normal distribution.
Specifically, Z-scores are vital for:
- Outlier Detection: Identifying unusually high or low values, much like spotting a single faulty sensor reading that throws off your entire diagnostic system.
- Comparing Data Sets: As we discussed, this is critical for comparing values across different scales or units.
- Probability Calculations: Z-scores are used in many statistical tests to determine the probability of an event occurring.
Key Specs and Main Parts: Z-Score Formula
The Z-score formula is deceptively simple but incredibly powerful:
Z = (X - μ) / σ
Let's break down the components, just like we'd dissect an engine diagram:
- Z: The Z-score itself. This is the number of standard deviations a data point is from the mean.
- X: The individual data point you want to standardize. Think of it as a specific sensor reading or the fuel efficiency of a single car.
- μ (mu): The population mean. This is the average of all the data points in your dataset. This would be the average fuel efficiency of all cars in a certain make and model.
- σ (sigma): The population standard deviation. This measures the spread or variability of the data around the mean. A higher standard deviation means the data is more spread out, like a wider range of fuel efficiencies observed in real-world driving conditions.
In R, we'll be using functions that calculate these values for us, so we don't need to do it by hand. However, understanding the underlying formula is essential.
How It Works: Calculating Z-Scores in R
Here's how to calculate Z-scores in R, step by step. This is analogous to following a detailed repair manual.
- Create Your Data: First, you need some data. Let's imagine you have data representing the horsepower of several modified engines:
horsepower <- c(250, 275, 300, 320, 260, 350, 280, 310) - Calculate the Mean: R's `mean()` function calculates the average:
mean_hp <- mean(horsepower) print(mean_hp) # Output: [1] 293.125 - Calculate the Standard Deviation: The `sd()` function calculates the standard deviation:
sd_hp <- sd(horsepower) print(sd_hp) # Output: [1] 31.36215 - Calculate the Z-Scores: Now, we apply the Z-score formula. We can do this in a single line of code using vectorized operations:
z_scores <- (horsepower - mean_hp) / sd_hp print(z_scores)The output will be a vector of Z-scores corresponding to each horsepower value.
Explanation: R automatically applies the formula to each element of the `horsepower` vector. This is a key feature of R that makes it efficient for data analysis. You can also create a function to do this:
calculate_z_score <- function(x, mean_val, sd_val) {
return((x - mean_val) / sd_val)
}
z_scores_function <- calculate_z_score(horsepower, mean_hp, sd_hp)
print(z_scores_function)
This approach is useful if you want to reuse the Z-score calculation in multiple places in your code.
Real-World Use: Basic Troubleshooting Tips
Let's say you've calculated Z-scores for a set of sensor readings from your car's engine. Here's how you might use them for troubleshooting:
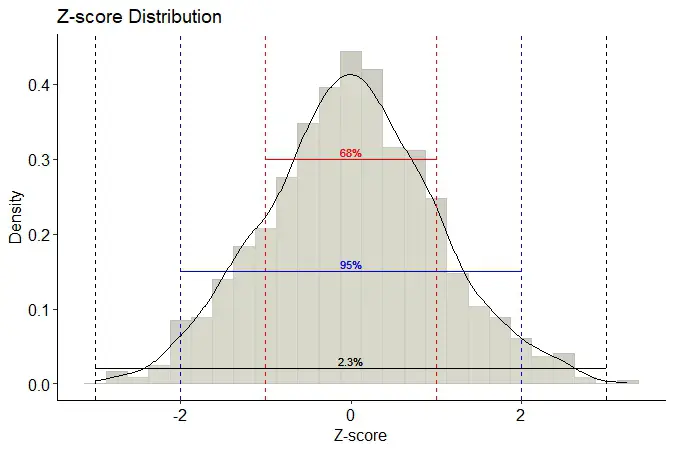
- Identifying Outliers: A common threshold for outliers is a Z-score greater than 2 or less than -2 (i.e., more than 2 standard deviations from the mean). If you find a sensor with a Z-score outside this range, it could indicate a faulty sensor or an actual problem with the engine. This is akin to seeing a value drastically different than expected during a diagnostic test.
- Comparing Sensor Readings: You might calculate Z-scores for the readings from different sensors to see if any are deviating significantly from their normal behavior. For example, if the Z-score for your oxygen sensor reading is much higher than usual, it might indicate a problem with the sensor or the fuel mixture.
Example: Suppose one of the horsepower values was significantly higher, say 400. Recalculating the Z-scores would highlight this outlier. This might indicate a problem (e.g., a misreading) or a genuine improvement (e.g., the engine is performing exceptionally well after a modification). You'd then investigate further.
Caveat: Remember that Z-scores assume a normal distribution. If your data is heavily skewed, Z-scores might not be the best way to identify outliers. Consider using other techniques like the interquartile range (IQR) method in such cases.
Safety: Data Integrity and Interpretation
While Z-scores themselves aren't inherently dangerous, misinterpreting them can lead to incorrect conclusions, much like misdiagnosing an engine problem could lead to further damage.
- Data Quality: Garbage in, garbage out. Ensure your data is accurate and clean before calculating Z-scores. Check for typos, missing values, and other errors.
- Context is Key: Don't blindly rely on Z-scores. Always consider the context of your data. A high Z-score might be perfectly normal in some situations.
- Sample Size: The accuracy of Z-scores depends on the size of your dataset. Small sample sizes can lead to unreliable results.
Beyond the Basics: Using R Packages for Z-Scores
While the basic formula is straightforward, R offers packages that can make Z-score calculations even easier and more robust. For instance, the `scale()` function provides a convenient way to standardize data:
scaled_horsepower <- scale(horsepower)
print(scaled_horsepower)
The `scale()` function automatically calculates the mean and standard deviation and then applies the Z-score formula. It returns a matrix with the scaled values. This is often faster and more convenient than calculating the mean and standard deviation separately.
Furthermore, packages like `outliers` offer more advanced outlier detection techniques that leverage Z-scores in combination with other statistical methods. These packages can be helpful for more complex data analysis scenarios.
In conclusion, understanding and calculating Z-scores in R is a valuable skill for anyone working with data. It allows you to standardize data, identify outliers, and compare values across different scales. It’s a powerful tool to add to your data analysis toolkit.
We have a comprehensive R script containing these examples and more. It includes error handling and edge cases, making it a reliable tool for your data analysis projects. You can download the script file to further refine your R data analysis and find Z score.
